Berlin - Es ist das wohl älteste ungelöste Problem der Mathematik: Im Jahr 972 tauchte das Rätsel der sogenannten kongruenten Zahlen erstmals in einem arabischen Manuskript auf. Im Laufe der Jahrhunderte sind Generationen von Mathematikern daran verzweifelt, darunter Genies wie Leonardo Fibonacci und Pierre de Fermat. Nun ist der Chinese Ye Tian der Lösung endlich ein Stück nähergekommen. Im Fachblatt Proceedings of the National Academy of Sciencesund auf der Preprint-Plattform arxiv.org berichtet er über die Lösung eines Spezialfalls.
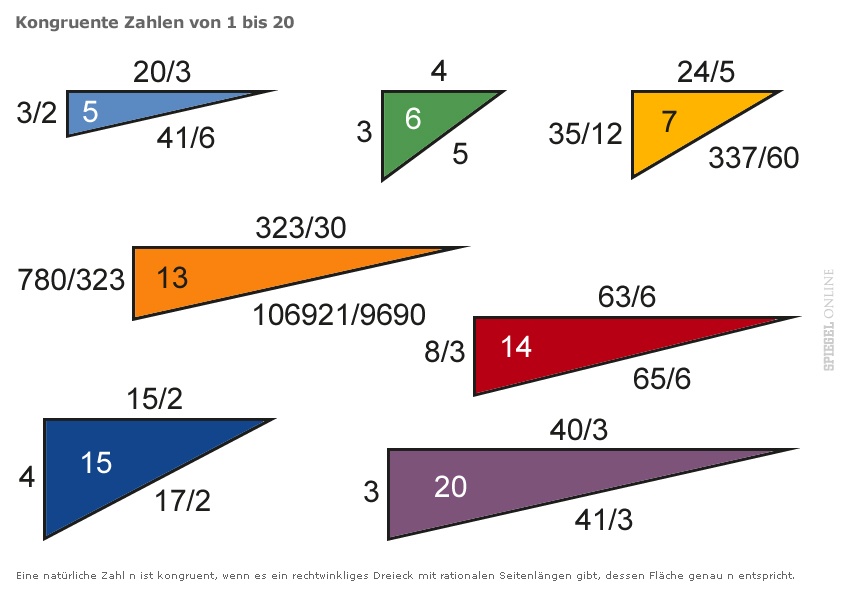
Das Problem gehört zur Zahlentheorie, mit der Mathematiker unter anderem die Geheimnisse von Primzahlen ergründen. Es hat aber auch einen direkten Bezug zur Geometrie. Eine natürliche Zahl n gilt als kongruent, wenn es ein rechtwinkliges Dreieck gibt, dessen Fläche genau n entspricht. Und wenn jede der drei Seitenlängen eine rationale Zahl ist - also ein Bruch zweier ganzer Zahlen p/q. Die 6 beispielsweise ist eine kongruente Zahl. Das zugehörige rechtwinklige Dreieck hat die Seitenlängen 3, 4 und 5, seine Fläche beträgt 3*4/2=6.

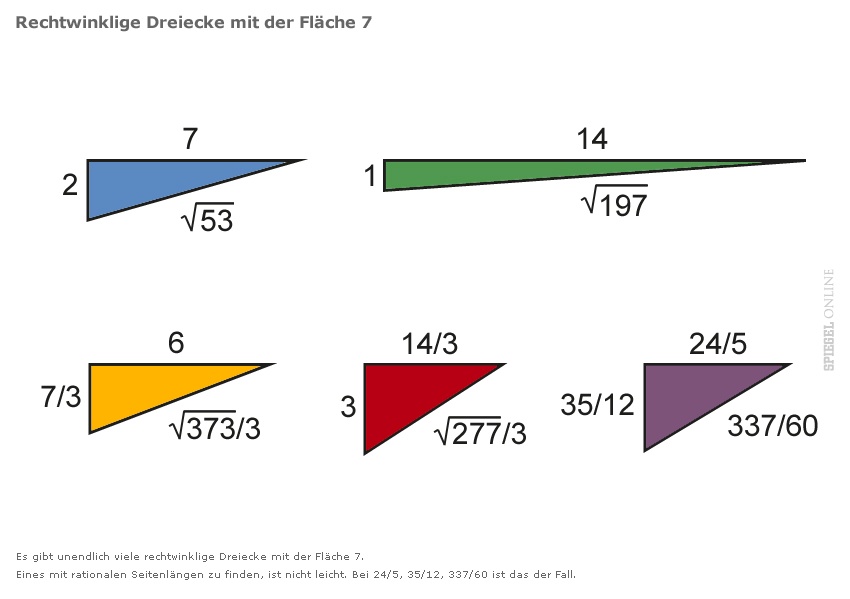
Wie aber findet man kongruente Zahlen? Woran erkennt man sie? Eine schier unlösbare Aufgabe, schließlich gibt es zu jeder Zahl unendlich viele rechtwinklige Dreiecke, die man theoretisch untersuchen muss. Beispiel 7: Die beiden Dreieckseiten am rechten Winkel können 14 und 1 lang sein - aber auch 7 und 2 oder 14/3 und 3 - stets ist die Fläche 7 (siehe Fotostrecke).
"Das wichtigste ungelöste Problem der Zahlentheorie"
Doch in allen drei Fällen ist die Länge der dritten Seite, Hypotenuse genannt, keine gebrochene, sondern eine irrationale Zahl - leicht auszurechnen mit dem Satz des Pythagoras. Trotzdem gibt es ein Dreieck mit der Fläche 7 und rationalen Seitenlängen, und zwar 288/60, 175/60 und 337/60.
Das Rätsel der kongruenten Zahlen ist eng verknüpft mit einer mathematischen Hypothese aus den sechziger Jahren - der Vermutung von Birch und Swinnerton-Dyer. Wenn diese zutrifft, dann müssen alle Zahlen der Form 8n+5, 8n+6 und 8n+7 für natürliche n0 kongruent sein. Aber bislang weiß niemand, ob die Vermutung, die sich mit elliptischen Kurven beschäftigt, wirklich stimmt.
"Das ist das wichtigste ungelöste Problem der Zahlentheorie", sagt John Coates von der Cambridge University. Im Jahr 2000 hat das amerikanische Clay Mathematics Institute sogar eine Million Dollar für die Lösung dieses Rätsels ausgelobt. Es gehört damit zu den sieben Millennium-Problemen, den schwierigsten Kopfnüssen für Mathematiker im dritten Jahrtausend. Geknackt wurde bislang erst ein einziges der Mammuträtsel: die Poincaré-Vermutung durch den Russen Grigorij Perelman im Jahr 2002.


Praktische Anwendung kongruenter Zahlen?
Ein Beispiel für eine solche kongruente Zahl ist die 15. Sie hat mit 3 und 5 zwei verschiedene Primfaktoren (k=2). Und 15 genügt der Form 8*1+7=15. Das dazu passende rechtwinklige Dreieck mit der Fläche 15 hat die Seitenlängen 15/2, 4 und 17/2.
Coates lobt Tians Arbeit als "Meilenstein in der Geschichte eines alten Problems", obwohl der Chinese nur einen Spezialfall gemeistert hat. "Wir sind auf dem Weg zur Lösung der Vermutung von Birch und Swinnerton-Dyer", sagt Hélène Esnault von der Freien Universität Berlin. Die Französin ist aber nicht ganz so optimistisch wie Coates: "Der Weg ist noch sehr weit."
Tian benutzt in seinem Beweis ähnliche Methoden wie Wiles beim Knacken des Großen Fermat: Er fahndet nach Punkten mit rationalen Koordinaten auf elliptischen Kurven. Das Rätsel der kongruenten Zahlen gilt sogar als die Inspirationsquelle für den Großen Fermatschen Satz. Als Fermat vor mehr als 350 Jahren bewies, dass 1 keine kongruente Zahl ist, folgerte er daraus auch, dass die Gleichung x4+y4=1 keine rationale Lösung mit x*y>0 haben kann. "Das führte ihn wahrscheinlich zu seiner berühmten Vermutung, dass die Gleichung xn+yn=1 für alle n>2 keine rationalen Lösungen größer null haben kann", sagt Coates.
Eine praktische Anwendung kongruenter Zahlen gebe es bislang keine, sagt der Mathematiker. "Es würde mich aber nicht überraschen, wenn später doch etwas dafür gefunden wird."
Das beste Beispiel dafür sind Primzahlen. Über Jahrhunderte galten sie als äußerst anspruchsvolle, aber weitgehend nutzlose Beschäftigung. Bis schließlich mit RSA ein Verschlüsselungssystem entwickelt wurde, das zwei möglichst große Primzahlen nutzt. Heute werden mit RSA sichere Internetverbindungen, Chips auf Reisepässen und Bankgeschäfte verschlüsselt.
Anmerkung der Redaktion: Der große Satz von Fermat lautet: Für natürliche Zahlen n>2 hat die Gleichung an+bn = cn keine Lösung mit natürlichen Zahlen a, b, c >0. Setzt man x=a/c und y=b/c, wird daraus: Für n>2 hat die Gleichung xn+yn = 1 keine Lösung mit rationalen Zahlen x,y >0.


Kommentare von Lesern
für unseren Newsletter an